RSM方法比较

某烟厂在分析影响单位废品剔除量的原因时，找到了两个因子：集中除尘风压、铲刀与细丝间隙，采用2因子2水平(加3个中心点)的全因子DOE,分析因子的最佳设置。集中除尘风压的高低水平设置为9500Pa、8500Pa，铲刀与细丝间隙高低水平设置为0.15cm、0.05cm，在进行了全因子DOE分析后发现弯曲项显著，为此决定采用响应曲面设计进行进一步分析。由于铲刀与细丝间隙因子不可能小于0.05，且每次试验的成本不太高。如何选择响应曲面设计方案，团队成员之间的意见不一致，你认为最合理的方案应该是：

A.CCC(中心复合序贯设计)

B.CCI(中心复合有界设计)

C.CCF(中心复合表面设计)

D.Box-Behnken设计

解：参考P426页，由于CCC（书中表格列名为CCD），在2因子的情况下，α取值为1.414，故星号点会超出原来实验设计的高低水平，故此项排除。

其他三项不存在超过高低水平的问题，都可使用，又因为，Box-Behnken设计的前提是实验成本高，除非非常注重试验次数，否则不采用。题目中明确说明实验成本不高，故D排除。

故只剩下B,C。CCI(中心复合有界设计)会将界限缩小至立方体内，原来的实验数据不能再用，CCF(中心复合表面设计)可以用原来的数据，CCF是成本较低的选择。

由于题目说成本不重要，那么就要对CCI与CCF进行比较以做出最佳选择。

一、从设计域的角度考虑

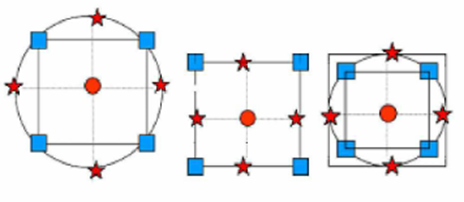
                        CCD                             CCF                              CCI

图一：三种设计示意图

从三种设计的示意图量来看，CCD和CCI设计域形状是球形域，具有旋转性，CCF是立方域，点子几乎都在表面。

如果试验者能够充分推测出优化目标存在于所研究的变量区域内,一般采用球形域。在许多实际情况下,当不能够在设计域的一个或者多个边界点上进行试验时,设计域与操作域相同,这时设计域是个立方体。也就是说如果过程不能在区域的一个或者多个立方体的顶点上操作（最佳组合不是高低水平的临界值）,那么不适宜采用CCF设计,这就留给试验者两个选择减少变量的区域产生一个新的CCF（把CCF也缩至界限内）,或者产生一个CCI。

二、设计预测能力方面

CCD和CCI都据有旋转性，CCF是立方体，不可旋转，另外由于CCD和CCI的因子水平有五种，而CCF只有三种，因此，球形域的模型预测精度会高于立方体的精度。几种实验设计的比较如下：

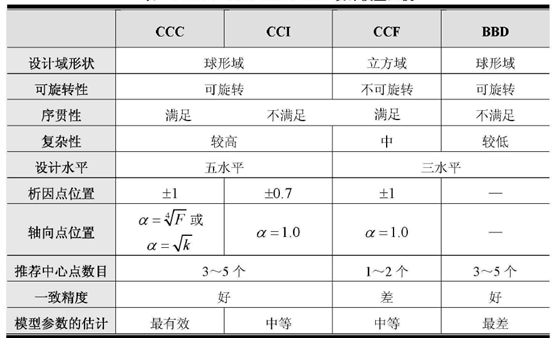
图二：4种RSM方法的比较

      结论:如果不在乎实验成本，并且最佳组合的条件不在因子水平的临界值（-1，1）,那么从理论上讲，CCI的因子水平更多，预测精度会更好些。因此本题建议选择CCI。